imaging::ShapeInterface Class Reference
[Shape Module]
Abstract class interface for shapes on a shape parameter manifold.
More...
#include <ShapeInterface.hpp>

Public Member Functions | |
| virtual void | exponential (const ublas::vector< float_t > &vector, ShapeInterface &shape) const =0 |
| virtual void | logarithm (const ShapeInterface &shape, ublas::vector< float_t > &vector) const =0 |
| virtual size_t | dimension () const =0 |
Detailed Description
Abstract class interface for shapes on a shape parameter manifold.
This class interface defines shapes, which are determined by parameters on a Riemannian manifold. I.e. every shape implements the Riemannian exponential which maps vectors to a shape in its neighborhood. The Riemannian logarithm maps shapes in this neighborhood back to its Riemannian coordinates with respect to the reference shape. If we denote the Riemannian manifold as 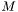 then every shape
then every shape 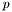 has to implement
has to implement
![\[ \textrm{Exp}_p: T_pM \rightarrow M \]](form_92.png)
and
![\[ \textrm{Log}_p: M \rightarrow T_pM \]](form_93.png)
The following example shows how this enables computations with shapes without the knowledge of details about the shape implementation. It computes the Riemannian logarithm with respect to the first shape of each of the remaining shapes. Then the mean of the logarithms is computed and mapped back to a shape. The function is fully generic, i.e. it does not know what the actual shapes it processes are.
template <class shape_t> void compute_mean(const std::vector<shape_t> & shapes, shape_t & mean_shape) { if(shapes.size() == 0) return; std::vector< ublas::vector<float_t> > logarithms(shapes.size() - 1); ublas::vector<float_t> logarithm_of_mean; shape_t & reference_shape = shapes[0]; // create an alias for the first shape // we call it reference_shape logarithm_of_mean = ublas::scalar_vector(reference_shape.dimension(), 0.0); // set the vector which will be the logarithm of the mean shape to zero ublas::vector<float_t> logarithm(reference_shape.dimension()); // will hold the logarithm of each shape in the loop below for(size_t i = 1; i < shapes.size(); ++i) { reference_shape.logarithm(shapes[i], logarithm); // computes the logarithm logarithm_of_mean += logarithm; // adds it to the scaled mean } logarithm_of_mean /= float_t(shapes.size()); // scales the mean correctly reference_shape.exponential(logarithm_of_mean, mean_shape); // computes the shape determined by logarithm_of_mean }
Member Function Documentation
| virtual void imaging::ShapeInterface::exponential | ( | const ublas::vector< float_t > & | vector, | |
| ShapeInterface & | shape | |||
| ) | const [pure virtual] |
Computes the Riemannian exponential of vector with respect to *this and stores the result in shape. In other words, shape is the projection of the tangent vector vector in the tangent space at the *this shape on the shape manifold.
Implemented in imaging::BsplineShape, imaging::Circle, imaging::MrepModel< position_t, atom_t, connection_t >, and imaging::MrepModel< imaging::Position2d, imaging::MrepAtom, imaging::imaging::MrepConnection< 2 > >.
| virtual void imaging::ShapeInterface::logarithm | ( | const ShapeInterface & | shape, | |
| ublas::vector< float_t > & | vector | |||
| ) | const [pure virtual] |
Computes the Riemannian logarithm of shape with respect to *this and stores the result in vector. In other words, vector is the projection of shape on the tangent space at the *this shape on the shape manifold.
Implemented in imaging::BsplineShape, imaging::Circle, imaging::MrepModel< position_t, atom_t, connection_t >, and imaging::MrepModel< imaging::Position2d, imaging::MrepAtom, imaging::imaging::MrepConnection< 2 > >.
| virtual size_t imaging::ShapeInterface::dimension | ( | ) | const [pure virtual] |
Returns the parametric dimension of the shape object. This is the same as the dimension of the shape manifold the shape belongs to. It should not be confused with the spatial dimension N.
Implemented in imaging::BsplineShape, imaging::Circle, imaging::MrepModel< position_t, atom_t, connection_t >, and imaging::MrepModel< imaging::Position2d, imaging::MrepAtom, imaging::imaging::MrepConnection< 2 > >.
The documentation for this class was generated from the following file:
- imaging2/shape/ShapeInterface.hpp
 1.5.5
1.5.5