Elastic Level Set Matching
In different imaging scenarios, such as medical and biological applications, several images of the same or similar objects are taken with the purpose of observing changes in them. However, the environment in which the acquisition is performed cannot be fully controlled, so one can not assume that the data will correspond point by point. Usually some deformation of the domain of definition of the images is necessary to align the data before comparing it. This problem is known as image registration. In many cases only the shape of an object (which may be extracted from images by segmentation techniques) is relevant. Registration in this case gives rise to the problem matching of two given surfaces. In this purely geometrical situation, what is sought is a map from one surface to another, which correctly matches shape features such as crests, valleys or bumps, and only introduces a low amount of distortion.
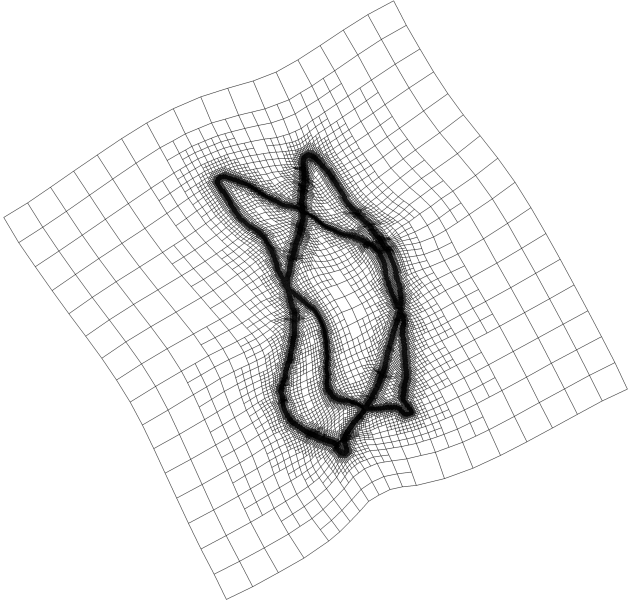
We have developed a model for the matching of surfaces represented by their signed distance functions. The model consists in an energy functional, which is to be minimized among deformations of a computational domain in which two given surfaces are embedded, producing a deformation that closely matches one of the surfaces to the other.
Our energy draws inspiration by the mathematical theory of nonlinear elasticity and reflects expected phenomena like resistance to compression and expansion of the surface and resistance to bending. For the modelling, our starting point is to consider the reference surface as a layer of an elastic material embedded in a block of another much softer isotropic elastic material, subject to a matching force that pushes it onto the template surface.
An advantage of this point of view is that physical material parameters which are relevant in applications may be effortlessly introduced. In fact, our formulation is dimension independent and may be used also in the case of curve matching.
Systematically exploting the geometry of the level sets, our model manages to balance full geometrical invariance with existence of global minimizers for any pair of surfaces of the same topology, while only including first derivatives of the unknown deformation. By introducing an explicit dependence on the deformed configuration, arguments of compensated compactness in varying directions can be applied to obtain weak lower semicontinuity of every term of the energy.
 |
 |
 |
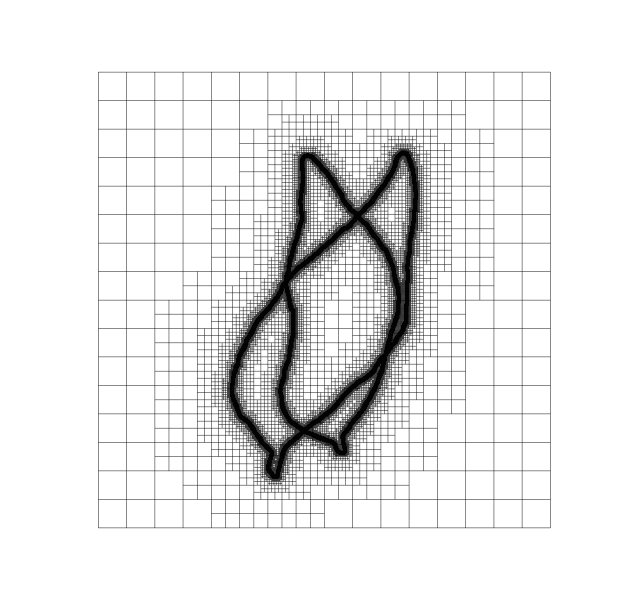
For the numerical implementation of the model, a multilinear finite element discretization and a multilevel minimization strategy have been considered. The use of hierarchichal adaptive grids refined around the given surfaces allows for efficient computations.
 |
 |
 |
 |
Contributors:
José A. Iglesias, Otmar Scherzer
Collaborators:
Martin Rumpf, Universität Bonn.
References:
- [1] J. A. Iglesias, M. Rumpf, and O. Scherzer; Efficient Matching of Implicit Shell Surfaces through Lower Semicontinuous Energies. In preparation, 2015.
- [2] J. A. Iglesias, B. Berkels, M. Rumpf, and O. Scherzer; A Thin Shell Approach to the Registration of Implicit Surfaces. VMV 2013: Vision, Modeling & Visualization, 89-96, 2013.
