imaging::EquationInterface< fem_types > Class Template Reference
[Equations]
Abstract base class of all PDEs to be solved using the finite element module.
More...
#include <EquationInterface.hpp>
Public Member Functions | |
| std::size_t | system_size () const |
| float_t | stiffness_matrix (std::size_t k, std::size_t l, std::size_t i, std::size_t j, std::size_t integrator_node, const FemKernel< fem_types > &kernel) const |
| float_t | force_vector (std::size_t k, std::size_t i, std::size_t integrator_node, const FemKernel< fem_types > &kernel) const |
| float_t | stiffness_matrix_at_boundary (std::size_t k, std::size_t l, std::size_t i, std::size_t j, std::size_t integrator_node, const FemKernel< fem_types > &kernel) const |
| float_t | force_vector_at_boundary (std::size_t k, std::size_t i, std::size_t integrator_node, const FemKernel< fem_types > &kernel) const |
| bool | sanity_check_stiffnesss_matrix (const FemKernel< fem_types > &kernel, std::string &error_message) const |
| bool | sanity_check_force_vector (const FemKernel< fem_types > &kernel, std::string &error_message) const |
Detailed Description
template<class fem_types>
class imaging::EquationInterface< fem_types >
Abstract base class of all PDEs to be solved using the finite element module.
To solve a (system of) PDEs with the imaging2 finite element module the user must design a class which implements the public members of this interface. It is also recommended to actually derive your class from EquationInterface. Then, an object of this class should be passed to Assembler::assemble(), Assembler::assemble_stiffness_matrix() or Assembler::assemble_force_vector() to compute the system of linear equation corresponding to the PDE.
The interface consists of four functions computing the coefficients in the stiffness matrix and the force vector respectively for a given element (determined by the current state of FemKernel). The function system_size() returns the number of equations in the system of PDEs.
For scalar PDEs it is advisable to make use of the interface SimpleEquationInterface. A simple equation can be transformed into a equation complying with EquationInterface by using SimpleEquationAdaptor.
To understand the parameters of the member function we give a (very technical) definition of the PDE problem this interface can model. Imagine that we are interested in the problem
![\[ \vec F(\vec u) = \vec f\,, \]](form_8.png)
where 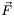 depends on the vector-valued function
depends on the vector-valued function 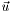 and its (higher order) derivative. We will rewrite this equation as
and its (higher order) derivative. We will rewrite this equation as
![\[ F^k\big((u^\ell)_\ell\big) = f^k\,, \]](form_11.png)
where 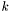 and
and 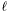 are indices in the range of the number of equations of the system. Furthermore we assume a basis
are indices in the range of the number of equations of the system. Furthermore we assume a basis 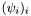 of shape functions on the problem domain, where each
of shape functions on the problem domain, where each 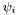 corresponds to a node on the grid. We define the vector-valued shape functions
corresponds to a node on the grid. We define the vector-valued shape functions 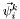 as
as
![\[ \big(\vec \psi_i^k\big)^m = \delta_{km} \psi_i\,. \]](form_17.png)
Following the common finite element approach we we express the unknown function 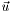 in terms of the shape functions, i.e.
in terms of the shape functions, i.e.
![\[ u^\ell = \sum_i u_i^\ell \psi_i\,. \]](form_18.png)
We hit the above equation with each of the test functions and integrate the resulting equations:
![\[ \int_\Omega \vec F(\vec u) \cdot \vec \psi_j^k = \int_\Omega \vec f \cdot \vec \psi_j^k\,. \]](form_19.png)
Then we can write the above equation in the following form:
![\[ \sum_i \sum_\ell u_i^\ell \int_\Omega F^{k\ell}_i (\vec u) \psi_j = \int_\Omega f^k \psi_j\,. \]](form_20.png)
Applying the Trace Theorem yields an extended version of this equation (to save symbols we re-use 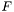 and
and 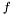 ; they are not the same functions as above):
; they are not the same functions as above):
![\[ \sum_i \sum_\ell u_i^\ell \Big(\underbrace{\int_\Omega F^{k\ell}_i(\vec u, \psi_j)}_{A^{k\ell}_{ij}} + \underbrace{\int_{\partial \Omega} G^{k\ell}_i(\vec u, \psi_j)}_{B^{k\ell}_{ij}} \Big) = \underbrace{\int_\Omega f^k(\psi_j)}_{a^k_j} + \underbrace{\int_{\partial \Omega} g^k(\psi_j)}_{b^k_j} \,. \]](form_23.png)
The parts 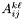 ,
, 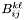 ,
, 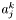 and
and 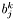 then correspond to the four members we mentioned in the introduction. Note that the above version of the equation is not uniquely determined. It depends on how the user applies the Trace Theorem, i.e. which parts of the equation you chose to transport to the boundary.
then correspond to the four members we mentioned in the introduction. Note that the above version of the equation is not uniquely determined. It depends on how the user applies the Trace Theorem, i.e. which parts of the equation you chose to transport to the boundary.
If she also must incorporate boundary conditions she might choose not to evaluate the equation on the boundary at all. This is equivalent to hit the equation with test functions with compact support only. Then, the terms 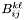 and
and 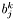 vanish at first. Instead, consider boundary conditions
vanish at first. Instead, consider boundary conditions
![\[ \vec G(\vec u) = \vec g\quad \textrm{on }\partial \Omega\,. \]](form_28.png)
and hit them with non-compactly supported test functions of the above form, i.e. test functions 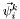 where
where 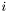 refers to a boundary node. Performing the same procedure as above on this equation adds the terms
refers to a boundary node. Performing the same procedure as above on this equation adds the terms 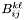 and
and 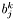 again (this time as a result of the boundary equation and not of the Trace Theorem).
again (this time as a result of the boundary equation and not of the Trace Theorem).
Member Function Documentation
| std::size_t imaging::EquationInterface< fem_types >::system_size | ( | ) | const |
Returns the number of equations in this system of PDEs. For scalar PDEs this is 1.
Reimplemented in imaging::SimpleEquationAdaptor< equation_t >.
| float_t imaging::EquationInterface< fem_types >::stiffness_matrix | ( | std::size_t | k, | |
| std::size_t | l, | |||
| std::size_t | i, | |||
| std::size_t | j, | |||
| std::size_t | integrator_node, | |||
| const FemKernel< fem_types > & | kernel | |||
| ) | const |
Computes the contribution of the integral 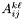 in integrator_node on the current element of kernel. The node indices i and j are node indices on the element, not global indices.
in integrator_node on the current element of kernel. The node indices i and j are node indices on the element, not global indices.
As kernel is set to the current element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via the indices i, j and integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).
Reimplemented in imaging::SimpleEquationAdaptor< equation_t >.
| float_t imaging::EquationInterface< fem_types >::force_vector | ( | std::size_t | k, | |
| std::size_t | i, | |||
| std::size_t | integrator_node, | |||
| const FemKernel< fem_types > & | kernel | |||
| ) | const |
Computes the contribution of the integral 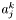 in integrator_node on the current element of kernel. The node index i is the node index on the element, not a global index.
in integrator_node on the current element of kernel. The node index i is the node index on the element, not a global index.
As kernel is set to the current element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via the indices i and integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).
Reimplemented in imaging::SimpleEquationAdaptor< equation_t >.
| float_t imaging::EquationInterface< fem_types >::stiffness_matrix_at_boundary | ( | std::size_t | k, | |
| std::size_t | l, | |||
| std::size_t | i, | |||
| std::size_t | j, | |||
| std::size_t | integrator_node, | |||
| const FemKernel< fem_types > & | kernel | |||
| ) | const |
Computes the contribution of the integral 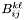 in integrator_node on the current boundary element of kernel. The node indices i and j are node indices on the element, not global indices.
in integrator_node on the current boundary element of kernel. The node indices i and j are node indices on the element, not global indices.
As kernel is set to the current boundary element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via the indices i, j and integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).
Reimplemented in imaging::SimpleEquationAdaptor< equation_t >.
| float_t imaging::EquationInterface< fem_types >::force_vector_at_boundary | ( | std::size_t | k, | |
| std::size_t | i, | |||
| std::size_t | integrator_node, | |||
| const FemKernel< fem_types > & | kernel | |||
| ) | const |
Computes the contribution of the integral 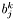 in integrator_node on the current element of kernel. The node index i is the node index on the element, not a global index.
in integrator_node on the current element of kernel. The node index i is the node index on the element, not a global index.
As kernel is set to the current boundary element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via the indices i and integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).
Reimplemented in imaging::SimpleEquationAdaptor< equation_t >.
| bool imaging::EquationInterface< fem_types >::sanity_check_stiffnesss_matrix | ( | const FemKernel< fem_types > & | kernel, | |
| std::string & | error_message | |||
| ) | const [inline] |
Checks if the dimension of the data corresponds to the dimension of the grid stored in kernel for the assembly of the stiffness matrix.
This function is called by the assemble routine right before the assembly of the stiffness matrix. It should return false if data which is necessary for the assembly of the stiffness matrix is still missing. Otherwise, return true;
| bool imaging::EquationInterface< fem_types >::sanity_check_force_vector | ( | const FemKernel< fem_types > & | kernel, | |
| std::string & | error_message | |||
| ) | const [inline] |
Checks if the dimension of the data corresponds to the dimension of the grid stored in kernel for the assembly of the force vector.
This function is called by the assemble routine right before the assembly of the force vector. It should return false if data which is necessary for the assembly of the force vector is still missing. Otherwise, return true;
Reimplemented in imaging::SimpleEquationAdaptor< equation_t >.
The documentation for this class was generated from the following file:
- imaging2/fem/equation/EquationInterface.hpp
 1.5.5
1.5.5