Viscoelastic Inverse Problems from Seismic to Medical Scale
We study the quantitative inverse problem for the reconstruction of heterogeneous material properties in non-invasive testing for medical and seismic imaging. The principle is to use measurements of mechanical waves on the partial boundary of the domain, from which the properties are inferred. The reconstruction of the stiffness properties of the medium serves to detect and diagnose diseases in medicine, and to identify subsurface seismic layers. Despite the differences between seismic and medical applications, such as the scale and the acquisition setups, both cases can use penetrating waves to probe the physical properties inside a body, as these waves convey information on the medium in which they propagate. This project further emphasizes the study of materials with attenuation, which increase the difficulty of wave simulations and imaging. Here, we rely on time-harmonic waves, which represent the convenient framework for such media.
 |
 |
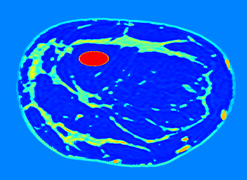 |
| Initial, reconstructed, and true wave-speed models for visco-acoustic breast imaging. The initial model is an homogeneous (constant) speed. | ||
 |
 |
| Initial model | Reconstruction |
 |
|
| True model | |
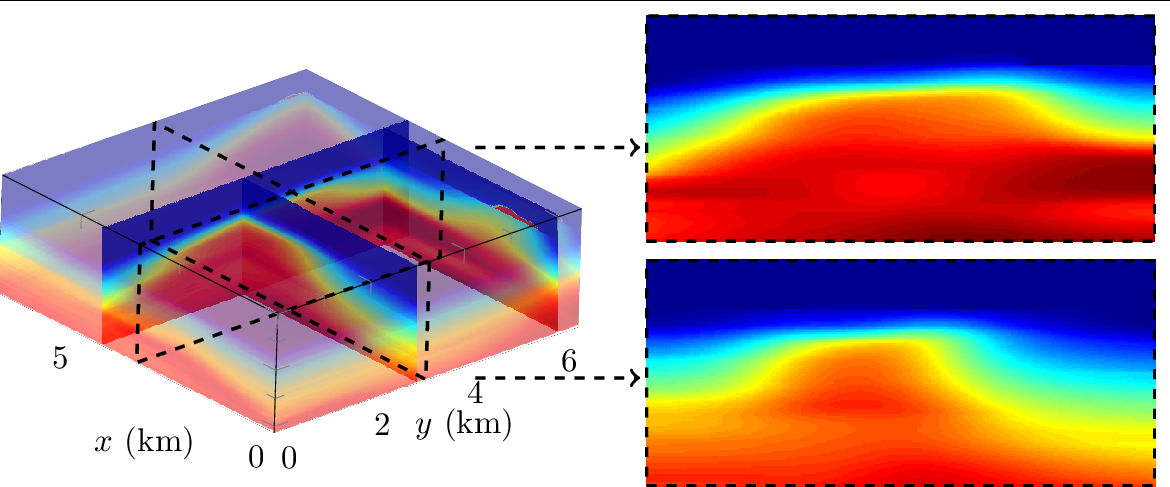
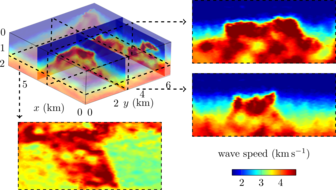
| Reconstruction of three-dimensional sub-surface wave-speed from surface measurements | |
Software: https://ffaucher.gitlab.io/hawen-website/
FWF project M-2791: Viscoelastic inverse problems from seismic to medical scale
Oskar Morgenstern-Platz 1, Room 07.128
1090 Wien, Austria

