Variational Methods for Imaging on Manifolds
The prime goals of this subproject of the ↗ National Research Network, Geometry + Simulation are to develop a mathematical analysis and numerical algorithms for variational methods for data, which are sparse, high dimensional, of multichannels (e.g. color data), and, in particular, defined on manifolds.
Our research on methods for filtering data of such kind is motivated from molecular biological applications, however not restricted to. The biological data serve as benchmark problems for the numerical algorithms to be developed during the course of the project. However, the developed mathematical analysis should be universally applicable.
The molecular biological application is the quantitative analysis of cells, movements and splitting in cells of model organisms, like the zebra-fish, during embryonic development. Our available molecular imaging data, which are recorded with 3D fluorescence microscopes, are spatio-temporal and of high resolution. An interesting characteristic of the data is that the relevant information, in this case fluorescence marked cells, is concentrated in a neighborhood of a manifold, the yolk (see Figure 1). This one varies between different individuals, but also within species. Moreover, it oscillates over observation time, and therefore has also a variation of geometry over time.
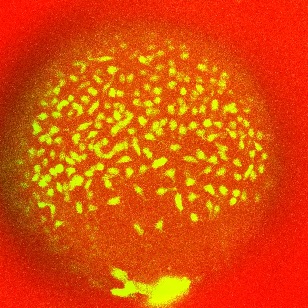
For analyzing this kind of biological data we propose a two step approach consisting in segmentation of the manifold (e.g. the yolk) first (note that the data are recorded with a 3D microscope which scans voxel by voxel), and then to apply variational image analysis methods to the data on the segmented manifold.
