New Inverse Problems of Super-Resolved Microscopy
Super-Resolved Fluorescence Microscopy (SRFM) and in particular Single Molecule Localization Microscopy (SMLM) have revolutionized the field of Biology by allowing for recording microscopic images of biological probes with a resolution of about 1 to 20 nanometers. This high resolution allows for visualization of single proteins, which play a key role in the transmission of diseases: For instance, the SARS-CoV-2 virus makes use of its spike glycoprotein to enter the host cells.
The basic experimental setup consists in chemically loading particular proteins with fluorescent dyes. SRFM records several microscopic images of immobilized samples and utilizes the complex interaction of laser light with fluorescent dyes for visualization via statistical processing.
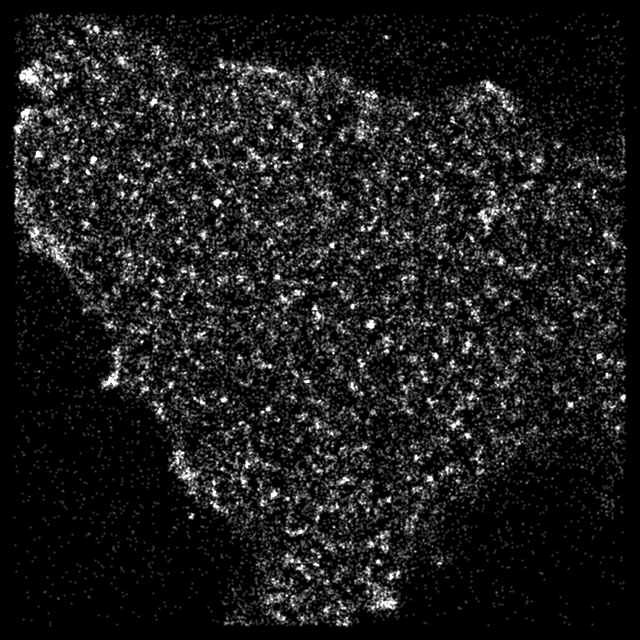 |
| Courtesy of Prof. Gerhard Schütz (TU Vienna). Typical SMLM-image of a cell. The spots show dyes, which have been calculated by averaging of detected localizations over frames. |
Our work is concerned with mathematical and computational aspects related to SRFM. Our developed mathematical analysis and computational algorithms are based on sophisticated mathematical models which take into account light propagation of fluorescent light in in-homogenuous media and describe the complex interaction of laser light with dye-molecules. The ultimate goal of this proposal is to extract in-homogenuous material parameters (like the density and permeability in the cell) from microscopic image sequences recorded with ultrahigh resolution imaging techniques.
We formulate new mathematical inverse problems of SRFM, where studies on its uniqueness and stability indicate feasibility of computational imaging in microscopic applications. In particular we want to find out the role and the effect of material in-homogenities on the accuracy of reconstructions of dyes locations. In contrast to existing computational techniques in SRFM, which reduce to image processing and statistical tasks for accurate localization of centers of dyes, we consider nonlinear inverse problems for reconstructing the material parameters of the probe.
