Integral Invariants
For shape matching and classification, an object, given by its shape, is compared with representative shapes of classes within a database. These problems are addressed in many areas of applied sciences such as computer vision, artificial intelligence, and pattern recognition.
The problems are tackled by a-priori assigning each object class within a database one or more typical representatives that capture the dominant features of the class. Then, the object under investigation is compared with the representative shapes using an appropriate notion of similarity. Common distance measures, such as the Hausdorff distance, are not appropriate, since they do not take into account the significance of dominant features. Additional shortcomings of global distance measures result from the fact that they are not invariant with respect to rigid motions. This invariance, however, is needed whenever the position in space of the object is not known a priori.
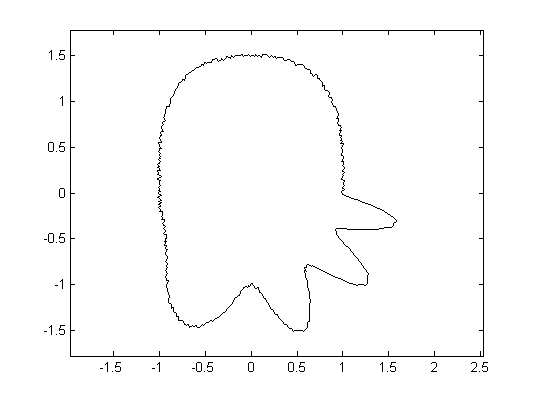
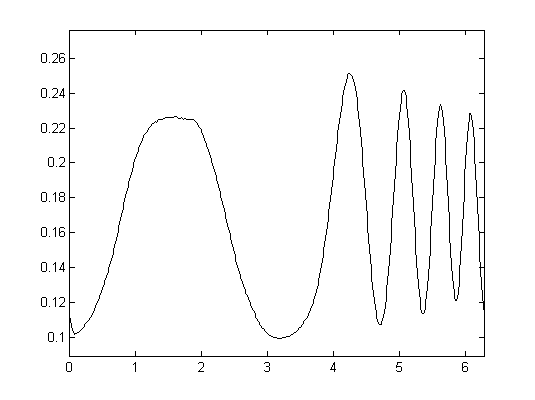
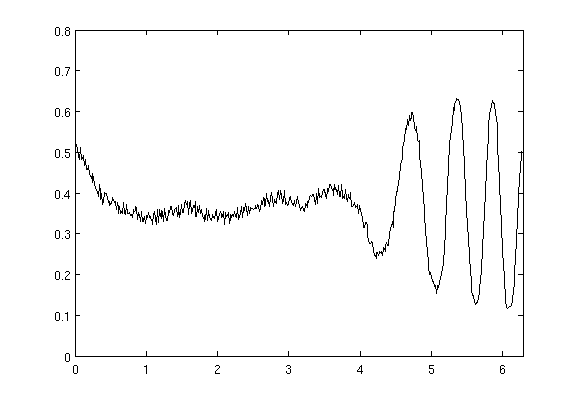
We consider descriptors of shapes which emphasize on peaks, edges, or ridges. These features can be expressed by differentials of the shape boundary (and thus are invariant under rigid body transformations). Differentials have been used successfully for shape matching and classification, but are difficult to handle numerically, since they are unstable with respect to noise. Alternatively, integral invariants have been proposed by Manay et al. [1], see also [3]. In comparison with differential invariants, a significant advantage of integral invariants is that by adopting the integration kernel they can be used selectively to capture dominating scales (features).
 |
 |
 |
 |
Although integral invariants have already been succesfully used in practice, several theoretical problems are still open (see [4] and [5]).
The first question is the theoretical possibility to uniquely reconstruct a shape from its integral invariant. A positive answer implies that an integral invariant uniquely determines a shape, and thus can be considered as a token. This question is even more involved when only partial data of integral invariants of an object are available; such a handicap can be observed if the object is partially occluded during data acquisition or the data of integral invariants has been damaged.
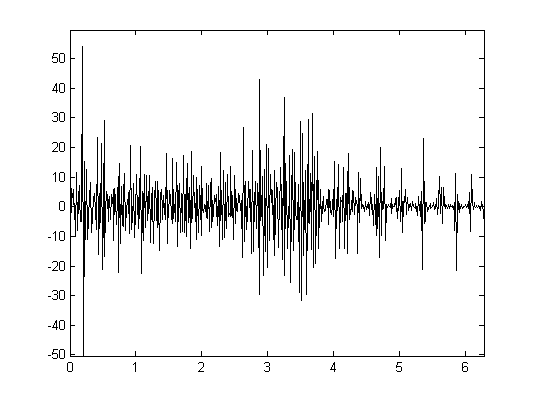
The second question concerns stability and the effect of noise on the shape matching and classification process. For this purpose appropriate distance measures of integral invariants have to be determined. Recently, we have developed novel variants of integral invariants for which partial answers to these questions could be derived. In the general framework, however, these questions could not yet be solved.
Acknowledgement:
The research on integral invariants is supported by the FWF (Austrian Science Fund) within the project S092-07.
Contributors:
Thomas Fidler, Markus Grasmair, Otmar Scherzer
References:
- [1] S. Manay, B. W. Hong, A. J. Yezzi and S. Soatto. Integral invariant signatures. In [2], pages 137–166.
- [2] H. Krim and A. Yezzi, Jr. Statistics and analysis of shapes. Birkhäuser, Boston, 2006.
- [3] H. Pottmann, J. Wallner, Q.-X. Huang and Y.-L. Yang. Integral invariants for robust geometry processing, 2007.
- [4] T. Fidler, M. Grasmair, H. Pottmann and O. Scherzer. Inverse problems of integral invariants and shape signatures. FSP 092: Joint Research Program of Industrial Geometry, 2007, 40, January, 2007. [PDF]
- [5] T. Fidler, M. Grasmair and O. Scherzer. Identifiability and reconstruction of shapes from integral invariants. Inverse Problems and Imaging 2(3):341-354 [PDF]
